Alcuni problemi su affinità e coniche

Problema 1 Dati tre punti allineati A, B e C, e due punti A’ e B’, costruire un punto C’ allineato con A’ e B’ tale che AB:AC=A’B’:A’C’. soluzione Creare una Macro che risolve il Problema 1 Scarica la Macro	Problema 2 Sono dati due piani XOY e X’O’Y’ che si corrispondono in una affinità. Dato un punto A del primo piano, costruire il suo trasformato A’ nella affinità assegnata. (Sfrutta la Macro del problema 1). soluzione Creare una Macro che risolve il Problema 2 Scarica la Macro
Problema 3 E’ assegnata una affinità che trasforma il triangolo ABC nel triangolo A’B’C’. Costruita una conica (con lo strumento “conica” di Cabri) trasformarla mediante l’affinità assegnata nella conica corrispondente, sfruttando la Macro del problema 2. Utilizza la costruzione per verificare che una affinità trasforma ellissi in ellissi, parabole in parabole e iperboli in iperboli. soluzione	Problema 4 E’ assegnata una affinità che trasforma il triangolo ABC nel triangolo AB’C’ (A è punto unito). Dato un punto P generico costruire il suo corrispondente P’ nell’affinità. soluzione Creare una macro che risolve il Problema 4. Scarica la Macro
Problema 5 E’ assegnata una affinità che trasforma il triangolo ABC nel triangolo ABC’ (A e B sono punti uniti). Dato un punto P generico costruire il suo corrispondente P’ nell’affinità. soluzione Creare una macro che risolve il problema 5 Scarica la Macro	Problema 6 Dopo aver tracciato una conica (con lo strumento “conica” di Cabri) trasformala mediante una affinità che abbia un punto unito sulla conica stessa, sfruttando la macro del problema 4. Trasformala poi anche attraverso una seconda affinità che abbia due punti uniti sulla conica, sfruttando la macro del problema 5. soluzione
Problema 7 Dimostrare che il luogo dei punti medi delle corde parallele di una parabola è una retta parallele all’asse della parabola. soluzione	Problema 8 Dimostrare una generalizzazione affine della formula di Archimede relativa al calcolo dell’area di un segmento parabolico ad una base perpendicolare all’asse (*). soluzione (*) Formula di Archimede: L’area del segmento parabolico a una base perpendicolare all’asse è 2/3 dell’area del rettangolo circoscritto. 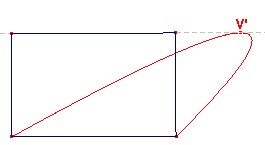Generalizzazione affine: L’area del segmento parabolico a una base è 2/3 dell’area del rettangolo in figura:
Problema 9 (...)	Problema 10 Dimostrare che l’area di una ellisse di semiassi lunghi rispettivamente a e b vale abp. soluzione
Problema 11 Dimostrare che la corda staccata da una retta secante su un’iperbole ha lo stesso punto medio del segmento individuato sugli asintoti.	Problema 12 Dimostrare che il punto di tangenza di una retta ad una iperbole divide a metà il segmento che gli asintoti staccano su di essa.
Problema 13 Dimostrare che il parallelogrammo che ha i lati sugli asintoti e un vertice sull’iperbole ha area costante. soluzione	Problema 14 Dimostrare che il triangolo formato dagli asintoti e da una tangente ad una iperbole ha area costante. soluzione